流体介质流过管路系统时,由于沿程摩擦产生能量损失,又由于局部阻力(阀门、三通、弯头、管径突然扩大与缩小)产生附加的能量损失。
在一个直径为DN的导管中,其压力损失△ρN的计算式如下:
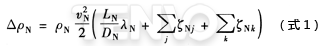

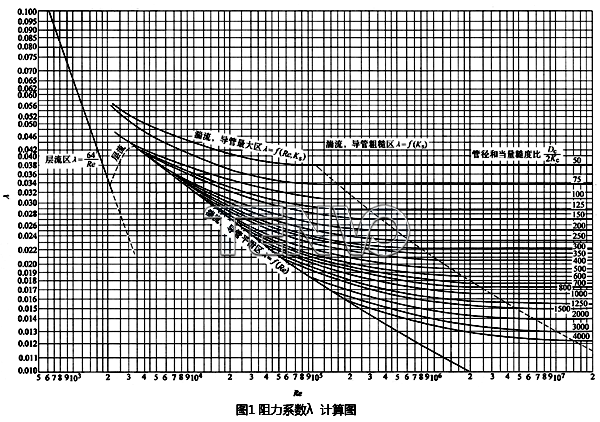
如果液体介质流过简单的管路,压力损失值可按实验确定的系数λ久进行理论计算,见图1。对于局部阻力,仅仅在简单的情况下进行理论计算,因为在大多数情况下,系数ζ是不同的,必须按不同情况通过实验来确定。实际上,系数ζ表示流体沿程阻力的动能损失。对于两个不同的结构或两种不同的工艺条件,除了偶然的情况外,水力阻力是不相等的,系数ζ也是不同的。
如果仅仅涉及到局部阻力,压力降的计算公式如下:
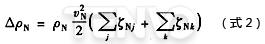
式中 vN——在局部阻力件之前或之后,按管径DN计算的流体平均速度,在某些情况下是指特定区的流速。
注意:在大多数情况下,ζ是对圆截面管道讲的。
1.局部阻力系数ζk
局部阻力分为阀门阻力和其他局部阻力。这样划分的目的,是便于深入研究通过阀门的介质流动。
(1)导管的流人和流出当容器与导管连接的时候,导管被安装在容器的出口或入口上,或者把导管的一头插入罐内引出导管,见图2和图3。图中已给出各种情况下的ζ值。
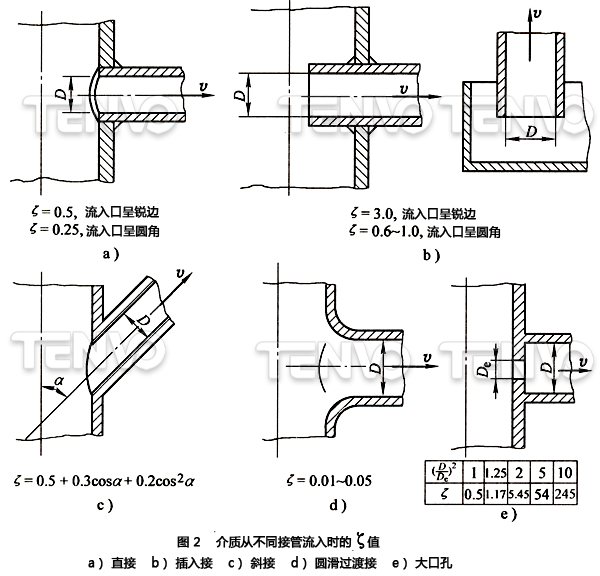
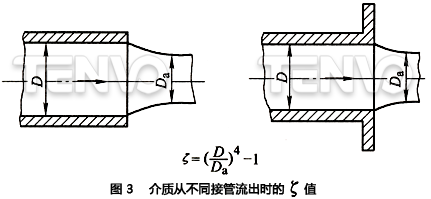
(2)流通截面的变化不同直径导管连接时需要连接件。这些连接件使截面积缓慢地或突然地扩大或缩小。下面介绍各种连接件的压力损失△p和流阻系数ζ的计算关系式。
1)突然扩大。如图4所示,如果压力损失主要是由于流通截面Al突然扩大,其计算公式如下:
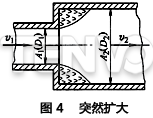
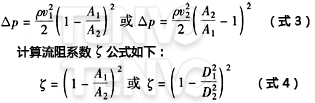
ζ值也可以查表1。
| (D1/D2)2 | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| ζ | 1 | 0.81 | 0.64 | 0.49 | 0.36 | 0.25 | 0.16 | 0.09 | 0.04 | 0.01 |
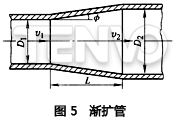
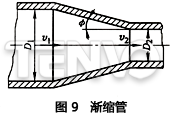
2)渐扩管。图5为介质通过渐扩管的简图。压力损失产生于介质对管壁的摩擦和流线的扩大。△p是几何尺寸Dl、D2、L和Φ的函数。
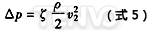
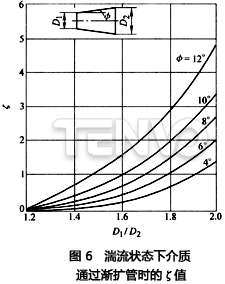
ζ可从图6中查得。这是对中等粗糙度管子的试验结果。
3)突然收缩。如图7所示,如果已知介质的收缩截面是A2,在这种情况下,压力损失的确定与突然扩大时相似。
计算压力损失△p时,可用式(5),而流阻系数ζ的计算如下:
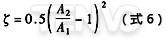
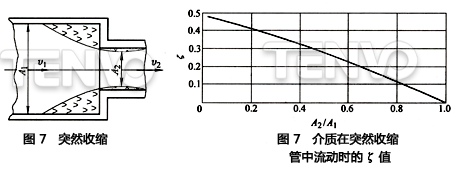
因为在大多数情况下,截面A2是不知道的,所以ζ是A2/A1的函数,如图8所示。它对应于进口处为锐边的突然收缩管中流动时的ζ值。
4)渐缩管。如图9所示的渐缩管,其压力损失比突然收缩的要小,其压力损失△p的计算如下:
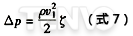
渐缩管的角度Φ=4°~10°时,ζ值可查表2,它是管子直径比的函数。
2.通过阀门的流阻系数
阀门可以切断、调节或者分配流过的介质。应对阀门进行下列分析:
1)确定阀门全开时产生的流阻或压力损失。
2)不同开度时的流阻系数或压力损失(主要是指调节阀)。
| D1/D2 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| ζ | 0.4 | 1.0 | 1.8 | 2.8 | 4.2 | 5.8 | 7.5 | 10 | 12 | 15 |
下面仅讨论切断阀。从经济的观点来看,希望阀的全开时阻力越小越好。因此,阀门的ζ值是一个非常重要的指标,也是分级的依据。
进一步研究阀门的特性,可以得出以下结论:
1)阀门的流阻影响系统性能。因为流阻存在,要求增高起点压力,或是降低用户的使用压力。
2)阀门的流体阻力值是介质参数和阀门结构的函数。
3)在较短的管路系统中,能量的总损失主要是由阀门压降引起的。
4)阀门结构的选择,不能仅考虑阀门起到启闭的作用,还必须使阀门的局部阻力尽可能地小。
通过式(1)可得出阀门压力损失的计算公式:
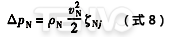
由上式可以看出,ζNj的量纲为1。它表示介质通过阀门时的能量损失程度。能量损失的原因是多种多样的,如方向的改变、流通面积的扩张或收缩、管壁的摩擦等。
图10示出几种调节阀的简图和介质能量损失的情况。要知道,即使对于一个构造简单的调节阀,要想通过理论计算得出ζNj值也是不可能的。ζNj值要通过试验确定。
下面介绍试验结果,以便为计算阀门的能量损失提供方便有用的数据。
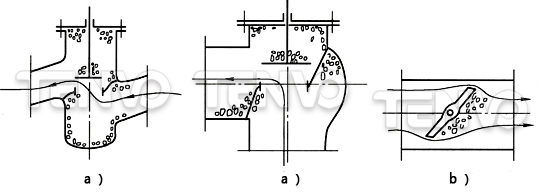
显然,应研究每种流动状态(层流、过渡流、湍流)下的ζNj值。但实际上,大多是湍流,故通常仅介绍湍流情况下的ζNj值。在雷诺数Re的函数中,ζNj值是个常数。





















